|
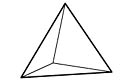
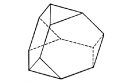
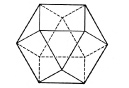
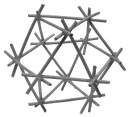
The weave cells shown so far relate to polygons; to triangles, squares, etc. with edges that bypass one another. It is possible also to translate three-dimensional solids, tetrahedra, octahedra, etc., into weave-like cells by again employing sticks as edges. I call these hybrid configurations weave-polyhedra or helix-polyhedra. Shown below: a weave-tetrahedron, a weave-truncated-tetrahedron, a weave-octahedron and a weave-cuboctahedron. Because of the helical bypass at their corners these three-dimensional structures have all the characteristics of the fabric weave cells except that each one is a spatial figure like its parent polyhedron.
|