|
Snelson has discovered a unique set of seven symmetry arrangements which permit identical circular magnets to link continuously on a sphere. They contain 2, 5, 8, 10, 14, 18 or 32 magnets. He uses these to represent magnetic arrangements where electrons link up to form systems of lower energy.
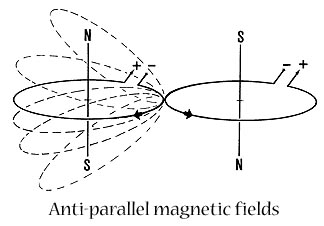
Snelson’s explanation for his magnetic structures: “In regard to the magnetic aspects of my model, it is often pointed out that the orbital magnetic field of the electron is puny — about 1/100th the strength of the electrostatic force, which would tend to push electrons away from one another. How, then, can such small magnetic fields urge them into proximity? What this over-looks is the atomic condition of electrons. Yes, they repel one another, and would perhaps prefer not to be so close together within the atom. But it is their lot to be confined by the nuclear electrical field which, electrically, they ‘balance out’. They make the otherwise positive nuclear sphere an electrical `gray’; that is, neutral. Now, this in no way diminishes nor abates the magnetic forces. These are no longer in a contest of strength with the repelling electrostatic forces. The nucleus has already forced the electrons to exist together. In this state, therefore, they must make the best of the situation and arrange their magnetic fields as economically as possible to conserve energy.” The small arrows near the circles on the previous page indicate the directions the electrons would move in order to give rise to adjacent antiparallel magnetic fields they operate in counter-rotating directions like gears Because these spherical forms have symmetry properties like polyhedra, with the planes of cubes and other geometrical shapes, they can form larger forms by joining at common magnetic faces. three such patterns are shown here.
|
| The five-magnet group can be extended in a honeycomb pattern. Magnetic polarities are reversed from cell to cell, linking one group tothe next. In all arrays, antiparallel linkages continue indefinitely to create an endless three-dimensional magnetic structure. | 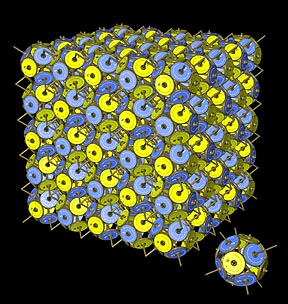 |
 |
Left, Snelson represents a plane of graphite with its carbon atoms arranged in hexagons. |