4 – THE ORIGIN OF THE MATTER-WAVE ELECTRON ORBIT IN SNELSON’S PICTURE
The Bohr-de Broglie model was a brilliant and original insight into how electrons perform within the atom. De Broglie proposed that just as light had been shown to have both a wave and a particle aspect, so might matter.

His now famous wave equation, indicated that an electron in a Bohr orbit racing around the atom’s nucleus would possess a wavelength of the right dimension to form standing waves. He envisioned the orbit as a pilot wave-continuous along the electron’s path. It was like a vibrating string–where whole, identical waves are formed. In his picture, the electron must “remember” where it had been as well as where it was going on Bohr’s energy spheres.

As in the illustration below, he showed that one standing wave could fit into the first shell, like a snake grabbing its tail. Two could form in the second shell, three in the third, etc.
As in Bohr’s model, de Broglie’s electron could move from one shell to another, through varying electrical levels, only by performing electrical work. This means taking in or giving off light. Normally the electron stayed on a shell at a constant distance from the nucleus. As the shells and orbits of Bohr’s model are quantized, so is the length of the wave of de Broglie’s electron at each shell. It grows longer as the electron moves to shells farther from the nucleus. This is because the electron travels more slowly in the larger shells, just as planets do in orbits more distant from the sun.

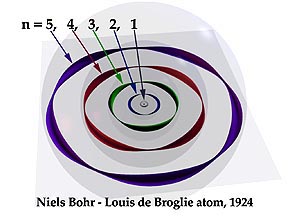
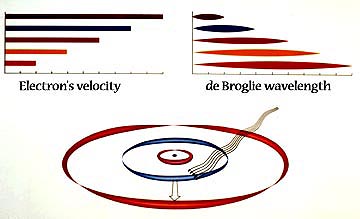
1913-1924 NIELS BOHR-LOUIS DE BROGLIE

HYDROGEN ATOM

Represented on the left is the relationship between the electron’s velocity and its de Broglie wavelength. The bars on the top symbolize velocity. As it reduces, the wave’s length (on the right) increases. These are not continuous changes. They are quantized in jumps within the atom.

As light enters, the electron absorbs a quantity large enough to lift it to the next shell. Its de Broglie wavelength increases. Its growth rate in the Bohr-de Broglie picture is additive, for astonishingly, at each new shell the wave is longer than it was in the previous shell by the dimension of the first shell wave. The second shell wave is twice as long as the first shell wave; the third shell wave is three times as long, etc.
The growth rate of the shells is not additive, however. They grow geometrically, by the second power. Therefore, to continue to surround the equator at each successive level the electron must include an additional whole wave in its orbit. One wave fits around the first shell, two waves surround the second shell, three around the third.

Because each shell has its own unique wavelength, it is interesting to see how a single wave, at each shell, would relate to the size of its proper shell. Shown here are the first five shells of the Bohr-de Broglie model.

Drawn on them are one-wave orbits composed of just one of the waves appropriate for each successive shell. Only at the ground level can the wave surround the shell’s equator.

OPTIONAL HALO ORBITS

IN SNELSON’S ATOM

The de Broglie standing wave is extended in Snelson’s model to provide the required orbital choices for the electron. These are shown as libration point, halo orbits. They come about by this principle: At the left is the de Broglie orbit of the hydrogen atom’s shell number two. Two standing waves surround the nucleus. Each wave is unique to this energy surface; twice as long as the wave in the first shell. Because this orbit is at the shells’ equator it has no preferred direction in respect to the nucleus. It can move over the electrical shell to occupy the entire sphere.
At the right is the optional one-wave halo orbit of Snelson’s model. Its single wave is identical to one of the waves of the two-wave state. Because it cannot surround the shell’s girth it travels only a small circle portion of it. It has achieved a direction in space, “reaching out” from the nucleus even though it remains on the same sphere as the equatorial orbit. Because its path is half as long, it completes its orbit at twice the speed of the two-wave state. This provides it with double the top-like angular momentum, and orbital magnetic force of the larger orbit.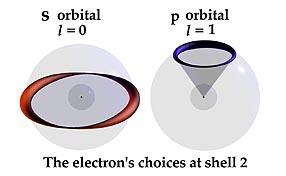

HOW MIGHT AN ELECTRON REMAIN

IN A SMALL CIRCLE HALO ORBIT?

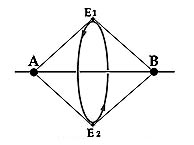
Niels Bohr originally introduced the idea of electrons in halo orbits, non-equatorial to the nucleus. This was shown in his proposed model of the Hydrogen molecule H2. He considered it as composed of two protons with a pair of shared electrons in a common orbit lying midway between the two nuclei.

A similar structure occurs in NASA’s libration-point satellite, the International Sun-Earth Explorer 3, which orbits in a place at a point of gravitational equilibrium in between the Earth and the Sun.
In Snelson’s model, in a complex atom with many electrons, those in the same shell provide one another with the supplemental force–their electrostatic repelling charge–which is needed to create a libration point electron orbit. Moreover, since the electrons are unable to interpenetrate one another’s matter-wave, this barrier is the associated phenomenon by which the orbits limit one another on the shells’ surface.
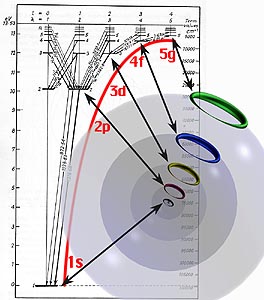
In the hydrogen atom there is no such supplemental force available to sustain the electron in a halo orbit. These states are therefore but momentary, transitory conditions. They can be likened to a “shelf” onto which the electron is deflected by incoming light from a direction. After landing at one of these levels where it is able to form a wave, it will fall at once back to a lower level.

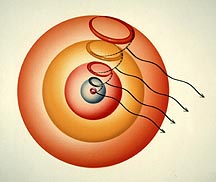
Shown here are the one-wave states for five consecutive shells, as the electron drops from one to the next with the emission of light of a certain color. The energy states in the electron’s fall would be from the 5g to 4f to 3d to 2p to the 1s ground state.
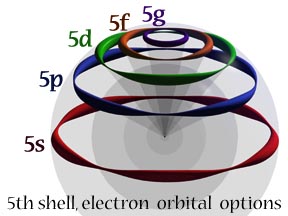
This picture represents the hydrogen atom’s fifth shell with the five possible excited states the electron can choose from, according to Snelson’s model. The orbit at the equator is de Broglie’s original orbit with its five standing waves. By maintaining the same length of the individual waves, the other four, libration-point orbits are created by the systematic removal of whole waves; one for each smaller orbit. This makes available a four-wave orbit (5p), a three-wave orbit (5d), a two-wave orbit (5f), and the final one-wave state (5g).

While the electron’s linear velocity does not change with each shorter pathway, the number of cycles per second is increased in jumps, to the maximum in the one-wave orbit. This has the effect of increasing the orbital angular momentum as well as the orbital magnetism.
« Previous
» Next